[알고리즘] 에라토스테네스의 체

에라토스테네스의 체

소수를 판별하는 알고리즘이다.

소수란 '양의 약수를 두 개만 가지는 자연수'를 의미하며 2, 3, 5, 7, 11, ... 등이 존재.

이러한 소수를 대량으로 빠르고 정확하게 구하는 방법이 에라토스 테네스의 체

 

 그리스의 수학자이자 지리학자인 에라토스테네스가 고안한 소수(素數)를 찾는 방법으로, 이 방법으로 소수를 찾으려면, 2부터 시작해 자연수를 차례로 쓴 다음, 2 이외의 2의 배수, 3 이외의 3의 배수, 5 이외의 5의 배수의 순서로 수를 지워나가 끝에 남는 수가 소수이다.

2부터 n까지의 숫자중에서 에라토스테네스의 체로 소수를 찾으려면, 2부터 시작해 n까지의 자연수를 차례로 쓴다. (2, 3, 4, ..., n)
그리고 2 이외의 2의 배수를 지운다(p=2). 이때 2가 최초의 소수가 된다.
그 다음 소수인 3을 제외한 3의 배수를 지운다(p=3).
이 방법을 다음에 지울 소수, 즉 p의 제곱이 n 보다 커질 때까지, 이 방법을 계속한다(p2≥n).

그러면 체로 친 것처럼 끝에 남는 수가 있다. 이 수가 바로 그 자신과 1 이외의 다른 수로는 나누어 떨어지지 않는 소수이고, 이렇게 소수를 찾는 방법을 에라토스테네스의 체라고 한다. 이 과정은 끝없이 계속되지만 20까지 자연수를 지워나가도 소수가 2, 3, 5, 7, 11, 13, 17, 19임을 쉽게 알 수 있다.

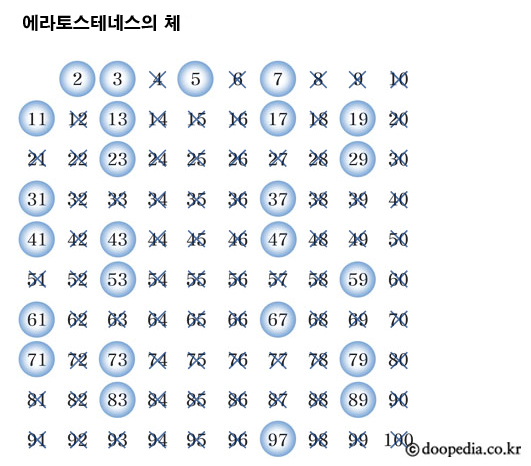
[네이버 지식백과] 에라토스테네스의 체 [Eratosthenes' sieve] (두산백과)

int number[100000];
 
int main()
{
    int n = 100;
    int answer=0;
 
 
    //2부터 시작해 자연수를 쓴다음 
    for (int i = 2; i <= n; i++)
    {
        if (number[i] == 1)
        {
            continue;  //i가 이미 체크된곳이라면 지나가
        }
        for (int j = i * 2; j <= n; j+=i)
        {
            number[j] = 1;   //i이외의 배수를 지운다
        }
    }
 
    for (int i = 2; i <= n; i++)
    {
        if (number[i] == 0)
        {
            cout << i<<endl;
        
        }
    }
 
 
    return 0;
 
 
}